今回は、OPTNET.INFO編集委員・前田智弘さん(光エレクトロニクス研究室)より、光複素振幅制御に関する最新技術を紹介していただきます。光複素振幅制御とは、光複素振幅の生成と検出を含む様々な技術の総称で、3Dディスプレイ、3D形状計測、光ファイバ通信の大容量化、生体計測など幅広い応用が期待されています。

イントロダクション
当研究室の研究テーマにおいて重要なキーワードのひとつに「光複素振幅」というものがあります.私たちはこの「光複素振幅」を制御することによる,3次元的な光情報処理(3Dディスプレイ,3D形状計測),光ファイバ通信の大容量化,生体計測などへの様々な応用を提案しています.本ページでは,まず光複素振幅がどのようなものなのかについて説明します.その後,光複素振幅制御技術の応用例をいくつか説明し,当研究室で提案している光複素振幅制御技術について一部を紹介します.
光複素振幅とは?
「光は粒子であり波動でもある」と言われるように,光は粒と波の性質を併せ持っています.岡本先生の研究グループでは,特に波としての性質に注目して研究を行っています.波としての光は電磁波の一種であるため,Maxwell方程式から導出される波動方程式の解によって表されます.ここで,一般的に「波」という言葉から連想される現象としては,水の波紋や音波などが挙げられます.これらの「波」は,図1のように伝搬する方向に対して(もしくは時間経過によって)振幅が上下しています.しかし,光の場合はどうでしょうか.もし水や音のように振幅が上下していたならば,空間的(もしくは時間的)に明暗を繰り返していることになり,非常にうっとうしいような気がします.(可視光の波長は380~780 nm,周波数は385~790 THzなので人間の目では到底捉えられませんが・・・.)実際のところ,光の強さは伝搬方向や時間に対して一定です.光は波なのになぜ振動していないのか.その答えは「複素振幅」にあります.

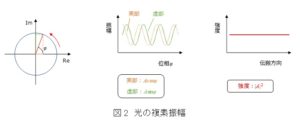
水や音の波は三角関数を使ってψ = Acosφ(Aは実数の振幅,φは位相)と書き表されます.一方,光を式で表すとψ = Aexp(iφ) = A(cosφ+isinφ)となります.虚数単位のiが入っていることからも,この式が複素数で表されていることが分かります.このように波の振動を複素数で表したものを複素振幅といいます.このとき,図2のように実部及び虚部はそれぞれ正弦波の形で振動をしていますが,光の強さ(強度)はI = |ψ|2 = |A|2と記述されるため,位置や時間の関数である位相に依存しないことが分かります.そのため,光の強度は伝搬方向や時間に対して一定となるのです.
どのような応用があるか
ここまでは光の複素振幅について説明しました.次は,光複素振幅を制御することでどのようなことが実現できるのかについて説明します.冒頭でも触れましたが,光の複素振幅を制御する技術の応用先は3次元情報処理,光通信や生体計測など多岐に渡ります.光通信や生体計測については他の方が説明してくださっていますので,このページでは3次元情報処理について代表的な例である3Dディスプレイと3次元形状計測について説明します.
① 3Dディスプレイ
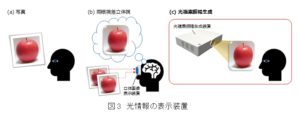
あなたが今まさに見ているパソコンもしくはスマートフォンのディスプレイ,他にもテレビや写真など,光情報の表示装置は私たちの身の回りに多数あります.しかし,それらの多くは光の”明るさ(強度)のみ”を再生しています.一方,光複素振幅を再生するということは,光の強度のみならず位相もまた再生することを意味します.この時,位相には光が伝搬してきた距離の情報が含まれます.すなわち,光複素振幅には物体の形状や複数の物体の奥行きの情報が含まれるため,光複素振幅を生成することで3Dディスプレイが実現できるのです.
立体的な画像を再生する技術と聞いて,裸眼立体視が可能な携帯ゲーム機や昨今話題のVR(Virtual Reality: 仮想現実)などを思い浮かべる方も多いかと思います.これらの機器では主に,「両眼視差立体視」という方式で立体感を演出しています.この方式では左右の目に異なる画像を見せ,画像の違いを脳内で処理することで奥行きを知覚します.ただし,このような立体視の方式では2次元画像に奥行きの情報を追加しているのですが,表示された立体像に対してユーザが自由に焦点を選択することができない,ユーザの視点が固定されているなど,様々な制約があります.このような制約から完全な3次元の情報を再生しているとは言えないため,両眼視差立体視は2.5次元の知覚とも言われます.一方,光複素振幅は光が持つすべての情報を有しています.そのため,ユーザが見たい部分に目の焦点を合わせることができ,見る角度によって立体を上下左右から見ることができるなど,3次元の情報を完全に再生する真の3Dディスプレイを実現することができます.
② 3D形状計測
先ほども述べたように,光複素振幅には物体の形状や複数の物体の奥行きといった情報が含まれます.そのため,物体から反射してきた光の複素振幅を取得することでその物体の3D形状を計測することができます.このとき,光の波長は数100 nmと大変短いため,奥行き方向に対してサブミクロンオーダーでの高精度な計測が可能です.
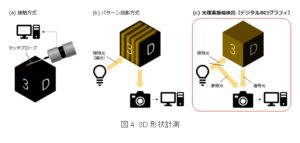
3D形状計測技術はタッチプローブを使用する接触方式や,縞状の光を照射してパターンの変化から物体の形状を推定するパターン投影方式などが存在します.後者のように光を使用する場合は,非接触(非破壊)での計測が可能であることから,近年産業分野で注目を集めています.デジタルホログラフィに代表される光複素振幅計測技術を用いた3D形状計測は,パターン投影方式と同様に光を利用する方式ですが,分解能に大きな違いがあります.パターン投影方式の分解能は,表示する縞の細かさや撮像素子の分解能にもよりますが,一般的に奥行き方向に対して数10ミクロンとされています.一方,デジタルホログラフィを利用した場合は,光源の波長レベル(数100 nm)以下の微小な傷や歪みまで検出することができます.
光複素振幅制御技術
① 光複素振幅の生成
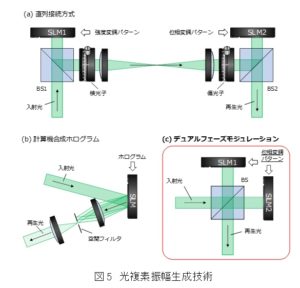
通常,光波の空間分布を制御するためには,空間光変調機(SLM: Spatial Light Modulator)が使用されます.しかし,SLMでは通常,光の強度もしくは位相のどちらか一方のみしか変調することができません.そのため,複素振幅を変調するためには強度変調と位相変調をそれぞれ別のSLMで処理する必要があります.ここで,2台のSLMを直列的に接続した場合,SLM間に距離があると伝搬による分布の変化生じてしまうため,通常はレンズによる結像系を2台のSLMの間に挿入します.この他にも付加的な光学素子が複数必要となることから,この手法では光学系の大型化が懸念されます.一方,複素振幅変調を1台のSLMで実現する手法として,計算機合成ホログラム(CGH: Computer-Generated Hologram)という手法も存在します.CGHは所望の複素振幅を持つ光波と平面波との干渉縞(ホログラム)をSLMに表示し,ホログラムからの+1次回折光として複素振幅を得る手法です.しかしながら,CGHはホログラムの表示にSLMの変調領域を過剰に消費してしまうことから,解像度の点に問題を抱えています.
そこで,光学系の小型化と高解像度の両立を目指し,当研究室ではデュアルフェーズモジュレーション(DPM: Dual-Phase Modulation)という手法を提案しています.DPMは2台の位相変調型SLMを並列的に配置した構成により複素振幅変調を実現します.ここで重要なのは,使用するSLMは2台とも「位相変調型」であるという点です.なぜ位相変調型のみで複素振幅変調が可能なのか.その秘密は光の干渉にあります.図5(c)のように,DPMではビームスプリッタ(BS)で光波を一度分岐し,各SLMで位相を変調した後に再度BSで合波します.これら2つの光波が重なり合うとき,光の干渉によって複素振幅の変調が実現されます.図6を見るとわかるように,DPMは直列接続方式よりも小型であり,なおかつSLMの解像度がそのまま再生像の解像度となることから,高解像度の変調も実現しています.
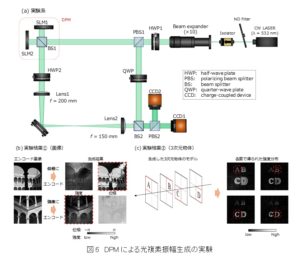
続いて,DPMによる光複素振幅の生成に関して,当研究室で行った実験について紹介します.実験に使用した光学素子の構成は図6(a)の通りです.まず,レーザ光を信号光と参照光の経路に分岐し,信号光に対してDPMによる複素振幅変調を与えます.変調後の光波は,変調前に分岐しておいた平面波と干渉させることで,その複素振幅をデジタルホログラフィにより取得しました.図6(b)は強度と位相にそれぞれ画像をエンコードした光複素振幅を生成した場合の実験結果です.それぞれエンコードされた画像が正確に再生されていることがわかります.また,図6(c)は奥行き方向に4枚の画像をずらして配置した,擬似的な3次元物体の光複素振幅を生成した場合の実験結果です.CCDに結像するレンズの焦点を各画像の面に合わせたときに,それぞれの文字が強度分布として明瞭に得られていることがわかります.
② 光複素振幅の検出
再三になりますが,光複素振幅は強度と位相によって成り立っています.この光複素振幅を検出しようにも,光の位相は私たちの目はおろか,CCDなどの撮像素子を用いても通常観測することができません.したがって,光複素振幅の検出には如何にして位相を可視化するかが課題となります.
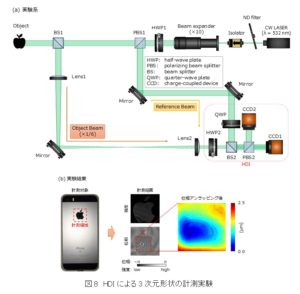
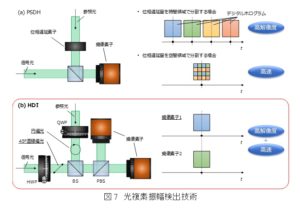
光の位相を可視化する代表的な手法として,位相シフトデジタルホログラフィ(PSDH: Phase-Shifting Digital Holography)という手法があります.PSDHは光の干渉の原理を利用しており,取得したい複素振幅を持つ光(信号光)の他に,信号光とコヒーレント(可干渉)な参照光を用意します.このとき,位相差を与えた参照光と信号光との干渉によって強度分布に生じる模様(干渉縞)を参照光に与える位相差を変化させながら複数回取得し,計算機による演算処理を行うことで位相を算出します.従来のPSDHでは参照光への位相差の与え方によって複数の形態が存在しますが,空間分解能と計測時間の両立は困難とされていました.これに対して,当研究室では複数の撮像素子の利用により撮像領域を分割することで高空間分解能と高速計測の両立を実現することができるHDI(Holographic-Diversity Interferometry)という手法を提案しています.HDIは偏光の特性を巧みに利用することで,参照光が位相差を持った複数の干渉縞を各撮像素子上に同時生成します.このとき,演算処理の際に補間などの必要がなく,撮像素子のピクセルをすべて有効に使用することができることから,高空間分解能での計測が可能です.
最後に,HDIによる光複素振幅の検出に関する実験として,3次元形状の計測を行った結果をお見せします.図8(a)が実験系で,計測対象はスマートフォン裏面の鏡面加工されたロゴマークです.計測によって得られた結果は図8(b)です.強度及び位相画像より,リンゴ型のロゴマークが計測されていることがわかります.ここで,得られた位相画像には位相値の包括(ラッピング)が生じており,このままでは深さ方向の情報を得られません.そこで,取得した位相画像に対して位相接続処理(アンラッピング)を施したものが右のカラー画像になります.ここで,スケールは位相から長さの次元に変換しています.アンラッピング後の画像を見ると,深さ方向に約2.5ミクロンほどの歪みがあることがわかります.一見すると平坦なものであっても,位相を計測することで微小な形状の変化を捉えることができるのです.